2  两步法折光改正模型原理

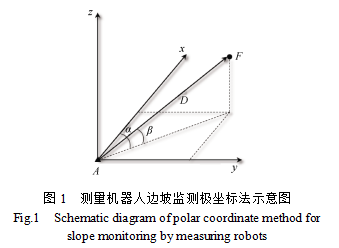
测量机器人边坡自动化监测系统通常采用极坐标法进行测量。以测站点A为原点架设测量机器人，测站铅垂方向为坐标z轴方向，x轴方向由测量机器人定向获得，建立左手系，如图1所示。位于测站点A的测量机器人对监测点F进行观测，获得的观测值包括斜距D、竖直角β和水平角α。则监测点F在测站坐标系中的坐标为

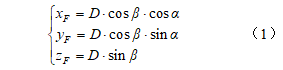
根据误差传播定律可知，监测点F的坐标值精度与斜距D、竖直角β和水平角α的观测精度均有关系。而上述观测值除仪器自身精度之外，还易受到气象因素的影响导致大气折光误差。为了削弱大气折光的影响，需要进行折光改正。传统的气象元素改正模型一般仅对斜距观测值进行了改正，忽略了角度折光误差。对于基准点差分改正模型，在利用若干校准基点求取相应差分改正系数时的处理方式不一，系数求取方法准确性较低，缺乏对不同监测点与校准基点之间空间位置关系的考虑。对此综合上述两类方法的特点，提出一种包括距离改正及坐标改正的两步法折光改正模型。两步法折光改正模型的具体实现流程如图2所示。其具体步骤如下。

1）观测数据获取

在测站点架设测量机器人并安装气象站，在监测区域的各监测点及稳定已知点安装棱镜观测目标。根据监测任务要求，程序自动控制测量机器人定期采集各监测点，以及已知点的水平角、竖直角、斜距与测站点的气象数据。

2）距离观测值的改正

利用气象站采集的气象数据进行第一步改正，即对斜距观测值进行气象改正。设测站到监测点或已知点的斜距观测值为D，根据气象站采集的大气温度、气压及相对湿度数据可计算气象改正数ΔD，改正后的距离可表示为。同时，利用改正后的斜距和原始的水平角α和竖直角观测值β计算监测点或已知点的三维坐标：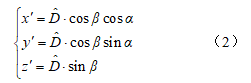

上述步骤在计算监测点的三维坐标时只对距离观测值进行了折光改正，未考虑角度观测值的折光误差。因此，其坐标仍包含角度折光误差的影响，需要对其进一步采取措施。

3）坐标差分值的计算

由于步骤2）推算的坐标已进行了距离折光改正，可认为推算坐标中仅包含影响角度观测值的折光误差，如大气垂向折光、旁向折光等。对于监测区域内的稳定已知点，设已知坐标为，i=1，2，…，N，则可根据各已知点通过步骤2）的推算坐标，计算受角度观测值折光误差影响的坐标差：

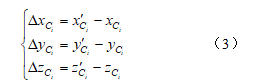
4）监测点的坐标差分

对各监测点进行第二步折光改正，设定用于折光改正的已知点，又称校准基点的数量K，依据相似相邻原理逐监测点搜索满足要求的校准基点参与坐标差分改正，得到监测点最终改正坐标，j=1，2，…，M。具体过程如下。

（1）以监测点j的三维推算坐标为球心，以初始设定的距离阈值如100 m为半径，搜索该范围内是否存在K个校准基点；如不满足该条件，则按设定距离步长阈值如20 m扩大搜索范围，直到搜索范围内存在足够数量的校准基点，如图3所示。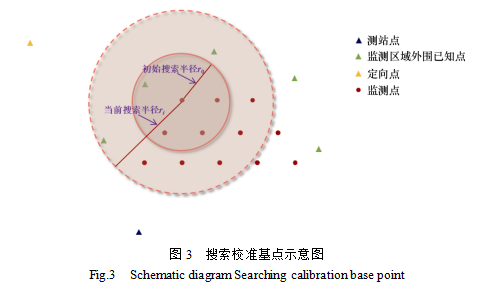

（2）以监测点j 到搜索到满足条件的各校准基点之间的距离Di（i=1，2，…，K）的倒数为权，按式（4）计算当前监测点j的三维坐标分量改正数： 

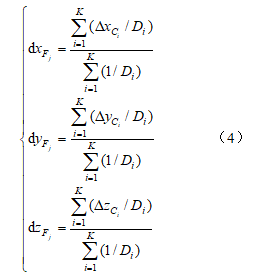
（3）将监测点j 的三维坐标分量改正数与其经距离改正的推算坐标相加，得到各监测点最终的改正三维坐标：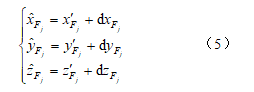

为了测试方法可行性，利用某水电站大坝边坡测量机器人自动化监测系统采集的观测数据展开分析。该监测系统采用了徕卡TM 50测量机器人，标称测角精度为0.5″，测距精度为0.6 mm±1×10–6 d（d为所测距离，m）。测量机器人安置于大坝右侧上游的观测房内，同时，在测站处设置了气象站同步采集大气温度、气压和相对湿度信息。选取了监测区域内RT04、RT06、RT07、RT08、RT09、RT10、RT11、RT12、RT14、RT15共10个监测点近8个月共计587期的监测数据展开分析。区域内可供选择的校准基点共有3个，分别为RT03、RT05、RT13。由于实验期间各监测点基本没有发生位移，因此，在评价本方法性能时以统计改正后各监测点X、Y、Z三个方向的中误差为依据。

3.1  校准基点数量的影响

本方法在距离改正的基础在搜索一定数量的邻近校准基点进行坐标改正，参与坐标改正的校准基点的数量会对最终改正结果产生影响。首先，对上述10个监测点的距离观测值进行第一步改正；其次，设定采用不同数量的校准基点执行监测点的第二步坐标改正。

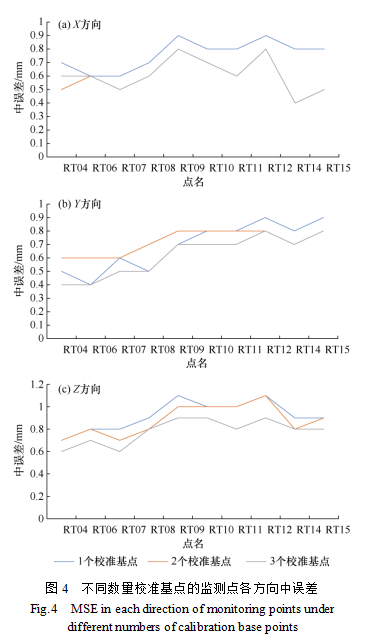
3.2  与典型方法的比较

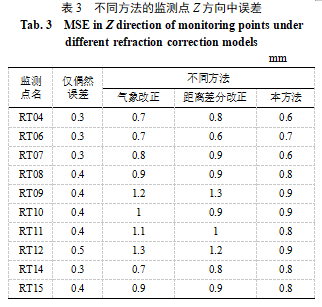
为了进一步分析方法有效性，对上述监测数据分别采用气象改正、距离差分改正方法及本方法处理后计算各监测点X、Y、Z三个方向的中误差。其中，气象改正方法利用了测站点同步采集的温度、气压和相对湿度信息，距离差分改正方法选择离监测点最近的已知点进行，本方法则是在气象改正的基础上选用3个校准基点进一步执行坐标改正。三种方法的计算结果如表1~3所示。

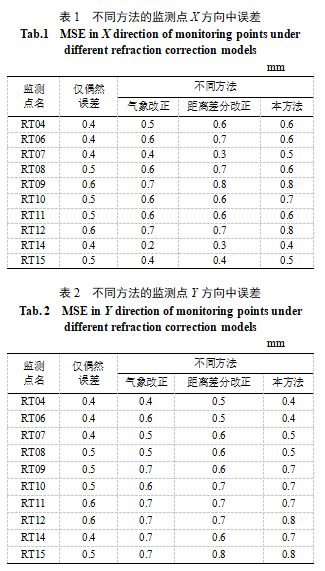
由表1~2可知，不同折光改正模型下各监测点在X、Y方向的中误差几乎无差异。这是因为气象改正、距离差分改正方法均是对监测点的距离观测值进行了改正，本方法虽然通过进一步的坐标差分改正，削弱气象因素对角度观测值的影响，而实际上水平角观测值受气象因素影响较小，因此，本方法在X、Y方向的改正效果与典型方法的差别不大。

由表3可知，本方法对各监测点Z方向的改正效果整体优于其他两种方法。主要原因在于气象改正、距离差分改正方法没有考虑角度，尤其是受气象因素影响较大的竖直角对监测结果的影响，而本方法在校准基点差分改正阶段有效地削弱了气象因素导致的竖直角误差对监测结果的影响。

综合来看，本方法在改正监测点Z方向的坐标结果上具有优势。